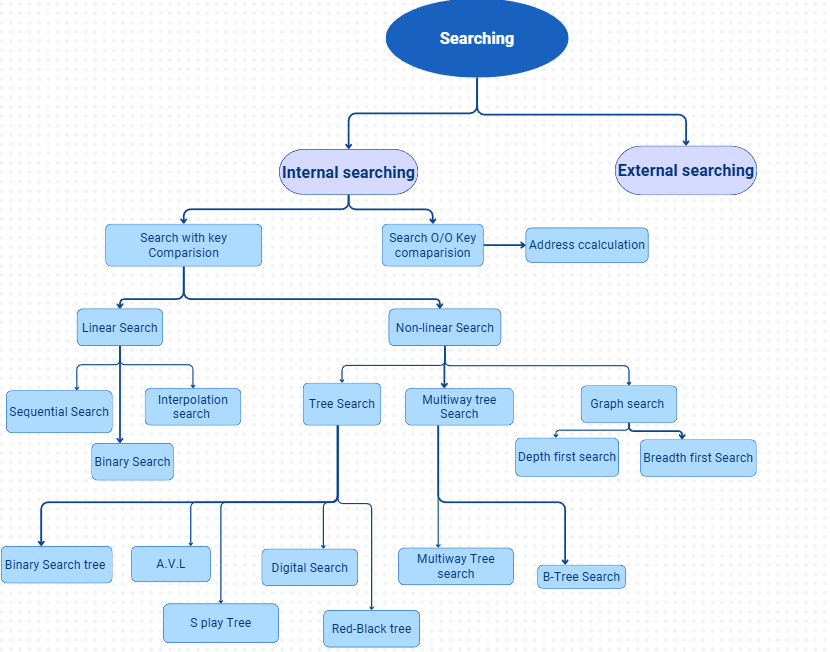
Searching Method :
Searching is the process of locating a particular( item or record )from a collection of data elements stored in various data structures like arrays, linked lists, trees, graphs, or databases, based on a given property or key.
The items may be stored in different forms such as:
- Records in a database
- Data in an array or linked list
- Text in files
- Nodes in a tree
- Vertices and edges in a graph
- Or any other type of search space
Linear search:
Linear search techniques are searching methods that involve data stored in a linear data structure such as an Array or a Linked List.
Hence, they are known as “Linear Search Methods.”
Important Linear Search Techniques:-
Searching methods are the processes used to find an item with specific properties from a collection of items.
- Sequential Search with Array
- Sequential Search with Linked List
- Primary Search
- Interpolation Search
Linear Search with Array:
This searching method is applicable when the data is stored in an array.
Basic Principle:
The algorithm starts searching from the beginning of the array and compares each element with the target value (key) one by one until:
- The required element(key) is found, or
- The end of the array is reached.
The algorithm terminates as soon as either of these conditions occurs.
Linear Search (Sequential Search) Algorithm
- Start
- Set i = 1
- Repeat Step 4 to Step 7 while i ≤ n
- If (K == A[i]) then
- Print “Successful search at location i”
- Go to Step 10 // Termination of a successful search
- Else
- i = i + 1 // Move to the next element
- End While
- Print “Unsuccessful search! Element not found.”
- Stop
Linear Search explaination:
Start searching from the first element of the array.
Compare each element with the key (K).
If a match is found → Successful search, print location and stop.
If you reach the end of the array without a match → Unsuccessful search.
Complexity Analysis of Linear Search:
| Case | Condition | Comparisons (T(n)) | Explanation |
|---|---|---|---|
| Best Case | Element found at first position | T(n) = 1 | Only one comparison needed |
| Worst Case | Element not present or found at last position | T(n) = n | Must check all elements |
| Average Case | Element is somewhere in middle | T(n) = (n + 1) / 2 | On average, half of array is checked |
Time Complexity:
- Best Case: O(1)
- Worst Case: O(n)
- Average Case: O(n)
Flowchart of Linear Search Algorithm:-
Steps of flowchart:
- Start
- Initialize
i = 1 - Input the array
A[1...n]and the key element (K) to be searched - Check condition:
i ≤ n ?- If NO ➜ Go to Step 9 (Element not found)
- If YES ➜ Go to Step 5
- Compare
K == A[i] ?- If YES ➜ Go to Step 7 (Successful search)
- If NO ➜ Go to Step 6
- Increment
i = i + 1- Go back to Step 4 (check next element).
- Print “Successful at location i”
- Stop
- Print “Unsuccessful search – Element not found
- Stop
Complexity Analysis of Linear Search Algorithm
The Linear Search Algorithm checks each element of the array sequentially until the desired key is found or the end of the array is reached.
Case 1: Best Case:-
Condition: The key element is found at the first position of the array.
Comparisons: Only 1 comparison is required.
Time Complexity:
T(n)=1⇒O(1)
Remark: The algorithm is most efficient in this case.
Case 2: Worst Case:-
Condition: The key element is not present in the array or is found at the last position.
Comparisons: All elements are compared, so n comparisons are needed.
Time Complexity:
T(n)=n⇒O(n)
Remark: This is the slowest case because the entire array must be scanned.
Case 3: Average Case:-
- Condition: The key element is present at any random position in the array.
- Assumption: Each position has an equal probability of containing the key.
That is, P1=P2=…=Pn=1/n. - To find an element at the i-th position,
the algorithm performs (i – 1) unsuccessful comparisons and 1 successful comparison.
So total comparisons = i

Remark: On average, half of the array elements are checked before finding the key.
Summary Table:-
| Case | Number of Comparisons (T(n)) | Asymptotic Complexity | Remark |
|---|---|---|---|
| Best Case | T(n) = 1 | O(1) | Key found at first position. |
| Worst Case | T(n) = n | O(n) | Key not found or at last position. |
| Average Case | T(n) = (n + 1)/2 | O(n) | Key found at any random position. |
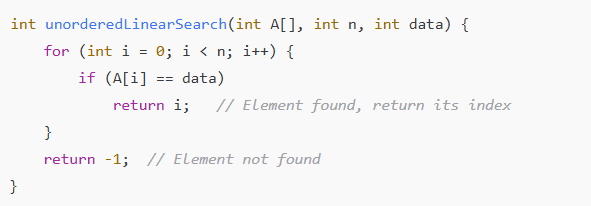
Unordered (Linear) Search:-
When the array is not sorted, we must scan the entire array element by element to check if the given element exists.
Algorithm (in C/C++ style):-
Summary:-
Start searching from the first element.
Compare each element with the key (data).
If found, return the index.
If not found after the loop, return -1.
Time Complexity:
- Best Case → O(1) (found at first position)
- Worst Case → O(n) (not found or last position)
- Average Case → O(n)
Ordered (Sorted) Linear Search:-
When the array is sorted in ascending order, we can stop searching early.
If we find an element greater than the key, we know the key cannot exist beyond that point.
Algorithm (in C/C++ style):-

Summary:
Start comparing elements one by one.
If the current element is equal to the key → success
If the current element is greater than the key → stop searching (because the list is sorted)
If we reach the end → key not found.
Time Complexity:
- Best Case → O(1).
- Worst Case → O(n)# because This is became in the worst case we need to scan.
- The complete array.But in the average Case it reduces the complexity even though growth rate is the same.
- Average Case → O(n).
Comparision Table:
| Feature | Unordered Linear Search | Ordered (Sorted) Linear Search |
|---|---|---|
| Data Order | Works on unsorted data | Works on sorted data |
| Search Method | Scan every element | Stop when element > key |
| Best Case | O(1) | O(1) |
| Worst Case | O(n) | O(n) (if element is last) |
| Advantage | Simple, works for all data | Slightly faster if data sorted |
| When to Use | When no order exists | When array is sorted |
